I apologise in advance for the hurried write up.
Abstract
We claim that we can measure the astronomical unit using nothing but the following image of Mercury transiting the sun as viewed from a satellite in near earth polar orbit. From this we can also determine the semimajor axis of Mercury's orbit and the orbital period of the satellite.
Methods and Conclusions
In order to solve this problem, we have to notice the sinusoidal motion of Mercury against the backdrop of the sun. This is an effect of the parallax using the a distance roughly the diameter of the Earth as a baseline. We also notice that there is a parallax effect on the sun that has been corrected in the image. As a result, the angle we measure by comparing the amplitude of the sine wave to the radius of the sun is the angle α between the centre of the sun and the apparent position of mercury against the sun. We then define β as half the angle from one position of the satellite at the pole to the other pole through the centre of the sun (see figure) and θ/2 as the parallactic angle of mercury compared to the backdrop of the stars.
It is easy to see from this diagram that π = α + β + π - θ/2 or θ/2 = α + β. Using small angle approximations for tangent, we get β = R/a and θ/2 = R/Δa with R the radius of the earth, a being the astronomical unit and Δa defined as the distance from the Earth to Mercury.
We also know the orbital period of Mercury which is 87 days and the orbital period of the Earth which is 365 days. Dividing, we get:
Then we use Kepler's 3rd Law we get:
Which gives us Δa = 0.62a.
Therefore, we have: 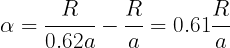
Drawing a circle on a printout of the satellite image that coincides with the border of the sun, we get the amplitude of the wave to be 1mm and the diameter of the disc to be 218mm. Using the ratio of these numbers and the fact that the angular diameter of the sun is 0.5 degrees, we get α = 0.00004 radians. We use R = 6378km and then get a = 9.71e12 cm which is roughly 0.65 of an actual astronomical unit.
We see that the semimajor axis of Mercury is a-Δa = 0.38a. We also have the orbital period of the satellite using Kepler's 3rd Law: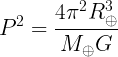 . We get P = 1:24:17 hours as the orbital period of TRACE the satellite (using the actual mass of the earth in our calculation).
. We get P = 1:24:17 hours as the orbital period of TRACE the satellite (using the actual mass of the earth in our calculation).
Discussion
Our result for the astronomical unit was off by a bit under 50% of the actual value. This error most likely came from the imprecise measurement of the diameter of the sun on the page and the amplitude of the sine wave across the sun. This was done by hand with no compass, which left a lot of room for error.
Acknowledgements
Thank you to Professor Johnson for providing the orbital period of Mercury, Jackie for pointing out the parallax of the sun, and Daniel for measuring the diameter of the circle.
Drawing a circle on a printout of the satellite image that coincides with the border of the sun, we get the amplitude of the wave to be 1mm and the diameter of the disc to be 218mm. Using the ratio of these numbers and the fact that the angular diameter of the sun is 0.5 degrees, we get α = 0.00004 radians. We use R = 6378km and then get a = 9.71e12 cm which is roughly 0.65 of an actual astronomical unit.
We see that the semimajor axis of Mercury is a-Δa = 0.38a. We also have the orbital period of the satellite using Kepler's 3rd Law:
Discussion
Our result for the astronomical unit was off by a bit under 50% of the actual value. This error most likely came from the imprecise measurement of the diameter of the sun on the page and the amplitude of the sine wave across the sun. This was done by hand with no compass, which left a lot of room for error.
Acknowledgements
Thank you to Professor Johnson for providing the orbital period of Mercury, Jackie for pointing out the parallax of the sun, and Daniel for measuring the diameter of the circle.



Very nice! Don't start off by apologizing.
Could you estimate the orbital period of TRACE using the image, and use this to measure the mass of the Earth?
Can you use the information you already solved for in the lab to determine the mass of the Sun?