Abstract
Considering the angular diameter of the sun and the astronomical unit, we can estimate the radius of the sun, the AU in solar diameters, and the mass of the sun using Kepler's 3rd law.
Methods
Applying basic trigonometric identities and taking the astronomical unit a to be the distances from us to the closest point of the sun to us (i.e., the centre of the circle we see from earth), we can see that:
Multiplying through by a we get a value for the radius of the sun. It is clear from here that if we divide a by twice the solar radius we can easily determine the answer to the second part of our question. Finally, we have Kepler's 3rd law:
Where P is the period of the earth and G = 6.7 x 10-8 dyne-cm2/g2. From here we can solve for the mass of the sun.
Results
Solving the first equation using a = 1.5 x 1013 cm we get the radius of the sun equal to 6.545 x 1010 cm which is very close to the actual value of 6.955 x 10107 s. Dividing, we get 1 AU = 114.6 solar diameters. Then, solving for the mass of the sun in Kepler's 3rd law with P = 3.154 x 107 s, we have the mass of the sun equal to 2.007 x 1033 g which is a surprisingly accurate number.
Results
Solving the first equation using a = 1.5 x 1013 cm we get the radius of the sun equal to 6.545 x 1010 cm which is very close to the actual value of 6.955 x 10107 s. Dividing, we get 1 AU = 114.6 solar diameters. Then, solving for the mass of the sun in Kepler's 3rd law with P = 3.154 x 107 s, we have the mass of the sun equal to 2.007 x 1033 g which is a surprisingly accurate number.

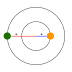
Can you calculate the AU in terms of solar diameters without knowing the AU or the radius of the Sun, only the angular diameter of the Sun?
Yes, actually. From the angular diameter we can easily find the angular radius theta. Then cot(theta)=(1 AU/R_sun). So 1AU = D_sun*cot(theta)/2 where D_sun is the solar diameter.