Second Authors: Nathan, Lauren
Introduction
Consider a problem of a planet orbiting a star. It's easy to see from Newtonian gravitation that they exert a force on one another. But then, how, according to Kepler's Third Law can we say the planet orbits the star alone? The star cannot remain fixed while feeling a force. In order for Newton's Laws to hold, we must say that they both orbit a mutual centre of mass. Using conservation of momentum, we can determine how far each body truly is from this centre of mass.
Methods
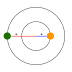
In order to balance forces, we notice that the planet and the star must be at opposite ends of their orbits at all times as seen in the following picture (not to scale). It follows from this that they have the same orbital period and the same angular velocity.
We know that linear momentum is equal around the centre of mass, such that:Dividing through, we get the relationship
Rearranging and using the mean semimajor axis, a, we can see that
Conclusion
We have shown here that star does indeed orbit the centre of mass, just as the planet does. However, looking at these equations carefully, we find that except for very massive planets, the semimajor axis of the star's orbit is roughly zero and the semimajor axis of the planet's orbit is roughly equal to the mean semimajor axis. As a result, we find that we can in fact use the assumptions implicit in Kepler's Law.


I like this a lot Eric! You really lay out the fundamentals of orbits very clearly.
When the other 2nd-year grad students and I were studying for the qual (major oral exam before our 2nd year), we got into a big argument about whether you could have two binary stars (or a star and a planet) in elliptical orbits about one another, where one of them has a different ellipticity than the other. Based on your findings here, what do you think?